függvény (f) a számítástanban halmazok közötti hozzárendelés, Általában az A és egy tetszőleges B halmaz közötti. Ez azt jelenti, hogy az A-ból a B-be ható f függvény az A halmaz minden eleméhez hozzárendeli a B halmaz egy elemét. f: A → B. Ha az a az A halmaz egy tetszőleges eleme, akkor az f(a) az f függvény egyetlen értéke az a-ban.

■ Függvénnyel kapcsolatos fogalmak:

▪ Értelmezési tartomány. Az f: A → B függvényben az A halmaz az f függvény értelmezési tartománya. Jele: D_f vagy D(f). Ekként ebben a függvényben a D(f) = A.

▪ Értékkészlet. A függvény értékkészlete; jele: Rf vagy R(f), a felvett értékek halmaza, amely a B halmaz része, de lehet azonos is vele. R(f) = {f (a): a ϵ D(f)} Ez azt jelenti, hogy az értékkészlet az f függvény összes értelmezési tartománybeli helyén felvett értékeinek a halmaza. ϵ = eleme. A képletben az a az értelmezési tartomány bármely elemét jelöli, az f(a) az f függvény a helyén felvett értéke. Az értékkészlet az f(a) értékek halmaza az összes lehetséges a értékre.

▪ Függvények egyenlősége. Két függvény, f és g, akkor egyelő, ha megegyezik az értelmezési tartományuk és azok minden pontja ugyanazt az értéket veszi fel.

■ A függvények megjelenítése: többféle. Megadhatjuk:

▪ Rendezett párok (az összekötött párok) között. A rendezett párok számpárok. f = {(0,0), (1,2). (2,4)… }. Ezt jelölik Venn-ábrázolással halmazábrákkal is, amelyben kör vagy lapított kör formájában rajzoljuk le a két halmazt (A-val és B-vel jelöljük őket), beleírjuk az elemeket, és nyilakkal jelöljük az összetartozókat.

▪ Táblázatban, amelyben vízszintes vonal két oldalán jelöljük az elemeket; az egyik oldal az x, a másik az y, és ezek mellé írjuk az elemeket:

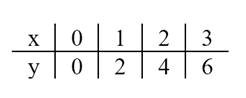
▪ A számpárokat elhelyezhetjük derékszögű →síkvonalas rendszerben.

▪ Képlettel. Ebben először azt jelöljük, hogy az első tagokból miként számoljuk a másodikat. A példánkban a második az elsőnek a kétszerese, vagyis: y = 2x.

A következőben jelölni kell, hogy mi lehet az első elem. Ha természetes számokkal dolgozunk, vagyis az x halmaz elemei természetes számok, amelyeknek a jele: N (ha a 0 is benne van: N₀), akkor így: xϵN (mivel ϵ az „eleme” viszonyt jelöli, az xϵN azt jelenti, hogy az x elem természetes szám).